Co to jest CAGR czyli jak nie dać się nabrać na średnią stopę zwrotu.

CAGR w świecie finansów jest znany każdemu profesjonaliście. Mówi nam on o realnym wyniku inwestycji. Jednak inwestorzy indywidualni i ludzie dbający o swoje finanse rzadko zwracają na niego uwagę. Wynika to z jego małej popularności poza branża. Jest to niefortunne, ponieważ prawdziwa stopa zwrotu to jedna z kluczowych informacji przy analizie potencjalnych inwestycji. Często pojawiają się na blogach i portalach internetowych informacje o takiej czy takiej stopie zwrotu. Jednak jak zaraz się przekonamy zawsze powinna nam się zapalać lampka ostrzegawcza, gdy nie jest wyraźnie sprecyzowane o jaką stopę zwrotu chodzi…

Średnia arytmetyczna a średnia geometryczna w inwestycjach:

Aby zobrazować o co mi chodzi posłużę się wyrazistym przykładem poniżej:

Mamy hipotetyczną czteroletnią inwestycję – zakup za 100 na koniec 2015 i sprzedaż w ostatnim dniu 2019 roku również po 100. Po drodze inwestycja zanotowała spadek o 50%, wzrost o 100%, ponowny spadek o 50% i ostateczny wzrost o 100%. Zaczynaliśmy od 100 i skończyliśmy na 100 (czyli nie zarobiliśmy nic). Ile zatem wyniosła nasza stopa zwrotu za okres pełnych 4 lat? Gratulacje! – nasza średnia (arytmetyczna) stopa zwrotu to +25%. Liczby przecież nie kłamią: (-50% + 100% – 50% + 100%)/4 = +25%. Tutaj dochodzimy do sedna – średnia (arytmetyczna) stopa zwrotu w finansach to nonsens i nie ma prawa bytu! Nie oddaje ona dobrze spadku na kapitale i nie uwzględnia procentu składanego. 

Dużo lepszym rozwiązaniem jest średnia geometryczna nazywana w finansach CAGR (Compound Annual Growth Rate – po polsku Skumulowany Roczny Wskaźnik Wzrostu, ale zostańmy przy CAGR, który jest powszechnie stosowany na świecie). Poniżej wzór CAGR dla inwestycji liczonych w latach:

WP – Wartość Początkowa

WK – Wartość Końcowa

n – Ilość lat inwestycji

Podstawiając dane naszej hipotetycznej inwestycji 

Lub dla fanów excela i arkuszy kalkulacyjnych: 

otrzymujemy wynik zgodny z rzeczywistością – roczna zannualizowana stopa zwrotu z 4 letniej inwestycji to 0%!

Zalety CAGR:

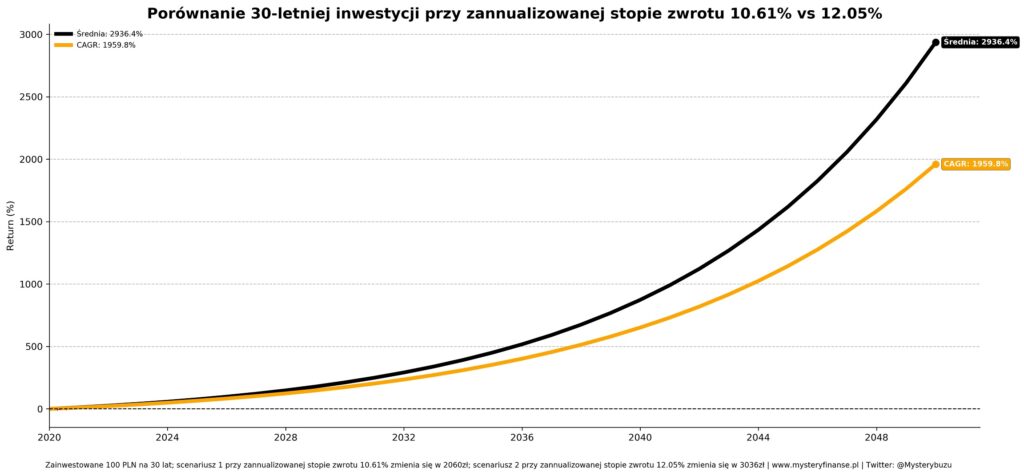
CAGR jest powszechnie stosowany w świecie finansów bo pozwala porównywać ze sobą różne klasy aktywów i potencjalne inwestycje. Kolejnym plusem jest fakt, że CAGR jest zawsze niższy niż średnia arytmetyczna stopa zwrotu więc znając prawdziwe liczby możemy mieć bardziej realistyczne oczekiwania przy budowaniu portfela. Poniżej bardzo dobre zestawienie różnicy między średnią a zannualizowaną stopą zwrotu dla amerykańskiego indeksu akcji S&P 500 za ostatnie 50 lat. 

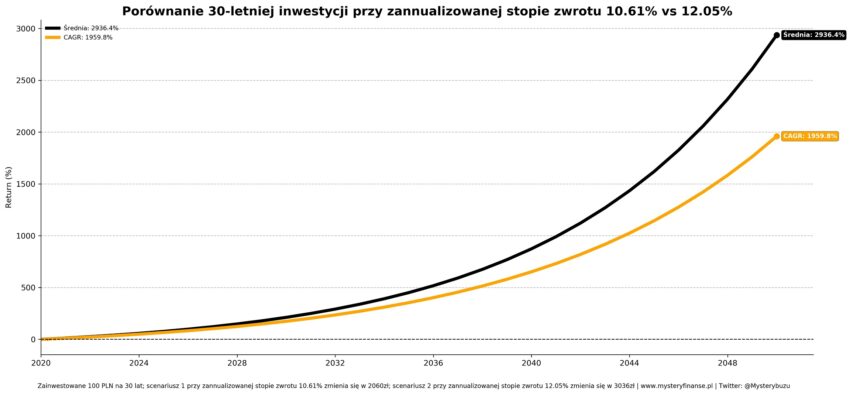
Wydawać by się mogło, że różnica o 1.44% powinna być pomijalna ale w rzeczywistości procent składany przez 30 lat sprawi, że zainwestowane 100 pln zamienia się w 2060 przy 10.61% lub 3036 przy 12.05%. Zatem 1.44% podnosi wycenę “portfela” aż o 47%!

Wady CAGR:

Podstawową jego wadą jest fakt, że wygładza wynik inwestycyjny i nie oddaje wahań (spadków) wyceny po drodze. Jak w przykładzie z S&P 500 powyżej mimo, że >10% rocznie jest świetnym wynikiem to nie daje się odczuć jakim “cierpieniem” było to osiągnięte. Aby otrzymać zwrot rynkowy trzeba było przetrzymać po drodze dwukrotne przepołowienie, krach z 1987 roku i wiele pomniejszych załamań – stąd tak zwana premia za ryzyko (premia rynkowa). Częściowym rozwiązaniem tego problemu jest analizowanie kroczącej x-letniej zannualizowanej stopy zwrotu, która pozwala ocenić najlepszy i najgorszy scenariusz w obranym horyzoncie inwestycyjnym – pokażę to za chwilę na przykładach. Kolejną wadą jest fakt, że formuła nie nadaje się do oceny portfela do którego dokładamy/wyjmujemy środki. Założeniem CAGR jest, że raz wpłacone (na początku inwestycji) pieniądze zostają w całości zainwestowane do wypłaty a ewentualne dochody są reinwestowane w aktywo bazowe. Rozwiązaniem tego problemu w finansach jest wewnętrzna stopa zwrotu (IRR dla przepływów regularnych lub XIRR dla przepływów nieregularnych), ale to temat bardziej skomplikowany i być może na jeden z następnych wpisów! 

Przyjrzyjmy się teraz prawdziwym wynikom inwestycyjnym aby zobaczyć jak prezentowała się “średnia stopa zwrotu” w stosunku do zannualizowanej średniej stopy (CAGR) i kroczącej zannualizowanej stopy zwrotu.

Wyniki inwestycyjne – WIG:

Powyżej jest 10 rocznych stóp zwrotu dla indeksu WIG od 2010 do 2019 i podsumowanie całego okresu:

• Średnia (arytmetyczna) roczna stopa zwrotu = 4.8%
• CAGR (start 39986, koniec 57833) = 3.8%

Powyżej wcześniej wspomniany i moim zdaniem najlepszy sposób do analizowania stóp zwrotu na wykresie – krocząca x-letnia zannualizowana roczna stopa zwrotu z inwestycji w osi czasu od początku 2010 do końca 2019 roku. Przykład przedstawia 5-letni horyzont inwestycyjny (a właściwie 1250 sesji giełdowych – 250 przyjęte na rok). Należy go odczytywać, że ostatni CAGR 2.4% (na końcu wykresu) mówi nam o tym, że gdybyśmy kupili indeks WIG na koniec roku 2014 i sprzedali końcem 2019 to zrealizowalibyśmy roczną stopę zwrotu na poziomie 2.4% (czyli 12.6% za cały okres). Najlepszy możliwy scenariusz miał miejsce w drugim kwartale 2012 roku – gdybyśmy wtedy kupili WIG i sprzedali 5 lat później to zrealizowalibyśmy CAGR 10.8% lub 67% za cały okres. Z kolei najgorszy możliwy scenariusz inwestycji 5-letniej miał miejsce początkiem roku 2011 – zakup w tym czasie dawał wynik 5 lat później na poziomie CAGR -2.3% lub całkowitą stratę -11%.

Wyniki inwestycyjne – Złoto:

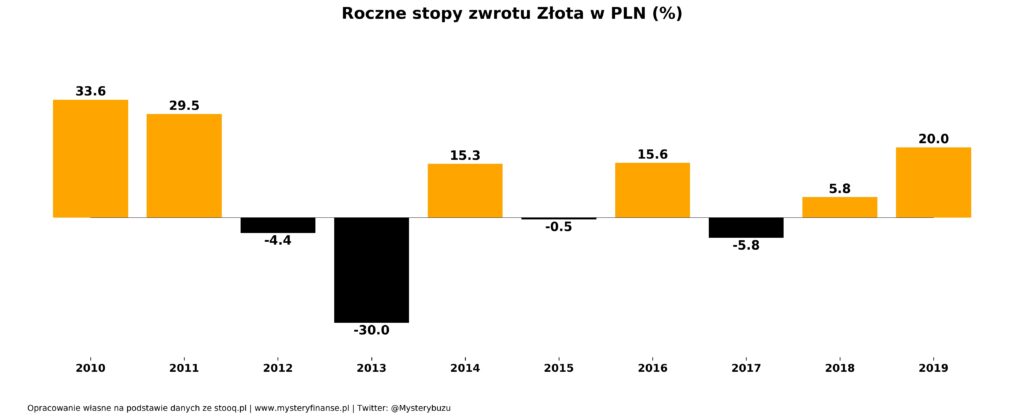
• Średnia (arytmetyczna) roczna stopa zwrotu = 7.9%
• CAGR (start 3140, koniec 57833) = 6.2%

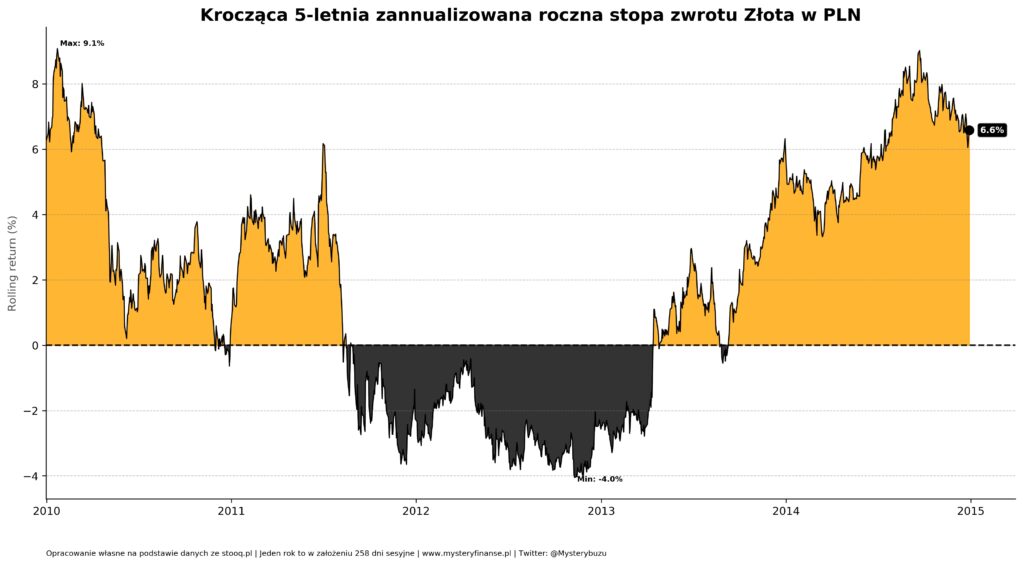
Warto tutaj zwrócić uwagę, że pomimo korzystnej dla złota narracji to jednak za ostatnie 10 lat (bez 2020!) była to bardziej ryzykowna inwestycja z większą szansą straty w horyzoncie 5-letnim. Najwyższy możliwy CAGR wyniósł 9.1% (vs WIG 10.8%) zaś najgorszy wyniki to -4% (vs WIG -2.3%). Chociaż ostatecznie za cały 10-letni okres wynik jest dużo lepszy od szerokiego rynku akcji polskich (złoto 6.2% / WIG 3.8%). 

Wyniki inwestycyjne – obligacje skarbowe (TBSP):

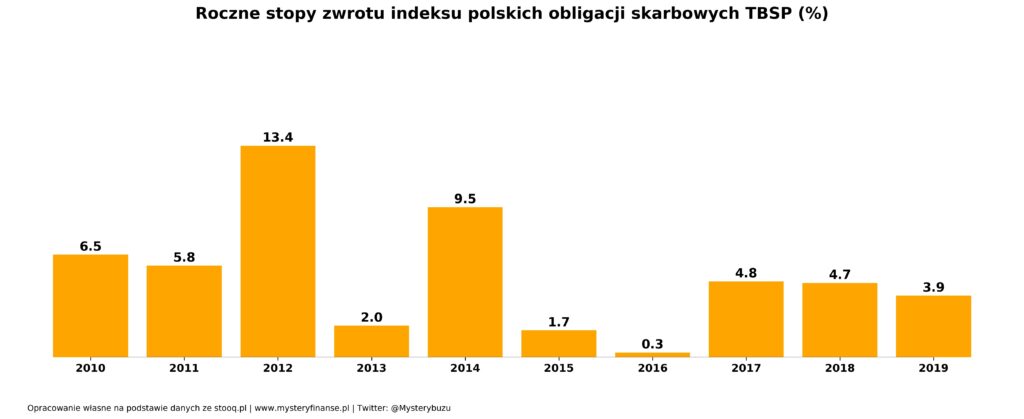
• Średnia (arytmetyczna) roczna stopa zwrotu = 5.3%
• CAGR (start 3140, koniec 57833) = 5.2%

Obligacje skarbowe nie miały ani jednego roku na minusie i jest to dobry przykład, żeby pokazać jak blisko w takim przypadku jest średnia roczna stopa zwrotu do CAGR (5.3% vs 5.2%). 

Podsumowanie

Jak widać na przykładach różnica między średnią arytmetyczną a geometryczną roczną stopą zwrotu może być znacząca i istotnie wpłynąć na wynik inwestycyjny.

Dlatego tak istotne jest aby zrozumieć jakie informacje otrzymujemy.

Jako ciekawostkę pokażę Wam jeszcze różnicę jak raportują swoje wyniki globalni zarządzający aktywami a ich polscy odpowiednicy.

Vanguard dla swojego ETFa FTSE All-World UCITS

BlackRock dla ETFa iShares Core MSCI World UCITS

PKO TFI dla funduszu Akcji Plus

Santander TFI dla funduszu Akcji Polskich

Obydwaj globalni gracze dają możliwość (a nawet z miejsca ustawione jako domyślne) zobaczenia zannualizowanej stopy zwrotu dla swoich instrumentów – chociaż Vanguard nieszczęśliwie nazywa je średnią roczną stopą zwrotu / average annual returns, ale nie ma wątpliwości, że dane przedstawiają CAGR. Tymczasem polskie TFI pokazują jedynie całkowity wynik z inwestycji (zagraniczne też mają tą informację w zakładce “Cumulative”). Dlaczego tak jest? – Nie wiem, ale się domyślam 😉

Pamiętajcie, że bez zannualizowanej rocznej stopy zwrotu ciężko jest porównywać instrumenty i alternatywne inwestycje między sobą oraz łatwiej ukryć bardzo niskie roczne stopy zwrotu…

Na koniec pamiętajcie aby być wyczulonym na informacje o wynikach inwestycyjnych i abyście nigdy nie dali się nabrać na to co jest zbyt piękne aby było prawdziwe (jak poniżej!)

Oczywiście średnia arytmetyczna zamiast średniej geometrycznej to nie jedyny sposób na “kłamanie” w finansach i temat jeszcze będzie wracał na blogu!

Mysterybuzu